Thermal conductivity and mathematical models

An attempt to build on last term's note, "I fiddled and tweaked my way to the initial logistic expression by using a computer in the possession of Brinando and Megan. They watched as I fumbled and fought my forward to a design that would behave in a way similar to their data. I explained what I was doing and why, including referring to the (x - h) portion of the graph. I gather one or both had MS 101 Algebra and Trigonometry, so they were not necessarily completely lost in my ramblings. I thought that interchange was valuable, that exercise was valuable. They were able to see their instructor struggle with a mathematical model, not have it quite right at first, and then iterate his way to a reasonable solution," did not go as well as hoped in the 8:00 lab.


I did not use a lap top as I did in the fall. Note two that all but one group saw an immediate and rapid linear rise in temperature until the peak temperature was reached. Only one group had that characteristic initial "flat" segment. My only thought for 11:00 is to attempt to get some temperature readings in the first minute, maybe at 30 seconds. I think I might also drag along my lap top and use that to chart the data.


 At 11:00 I used the lap top and began on a 30 second timing. Even with this a couple groups had no initial "flat" segment - by 30 seconds the temperature was already rising. Using the lap top I was able to finesse the equation, but ultimately this did not lead to anything more than "sometimes you can see things you do not understand from a mountaintop."

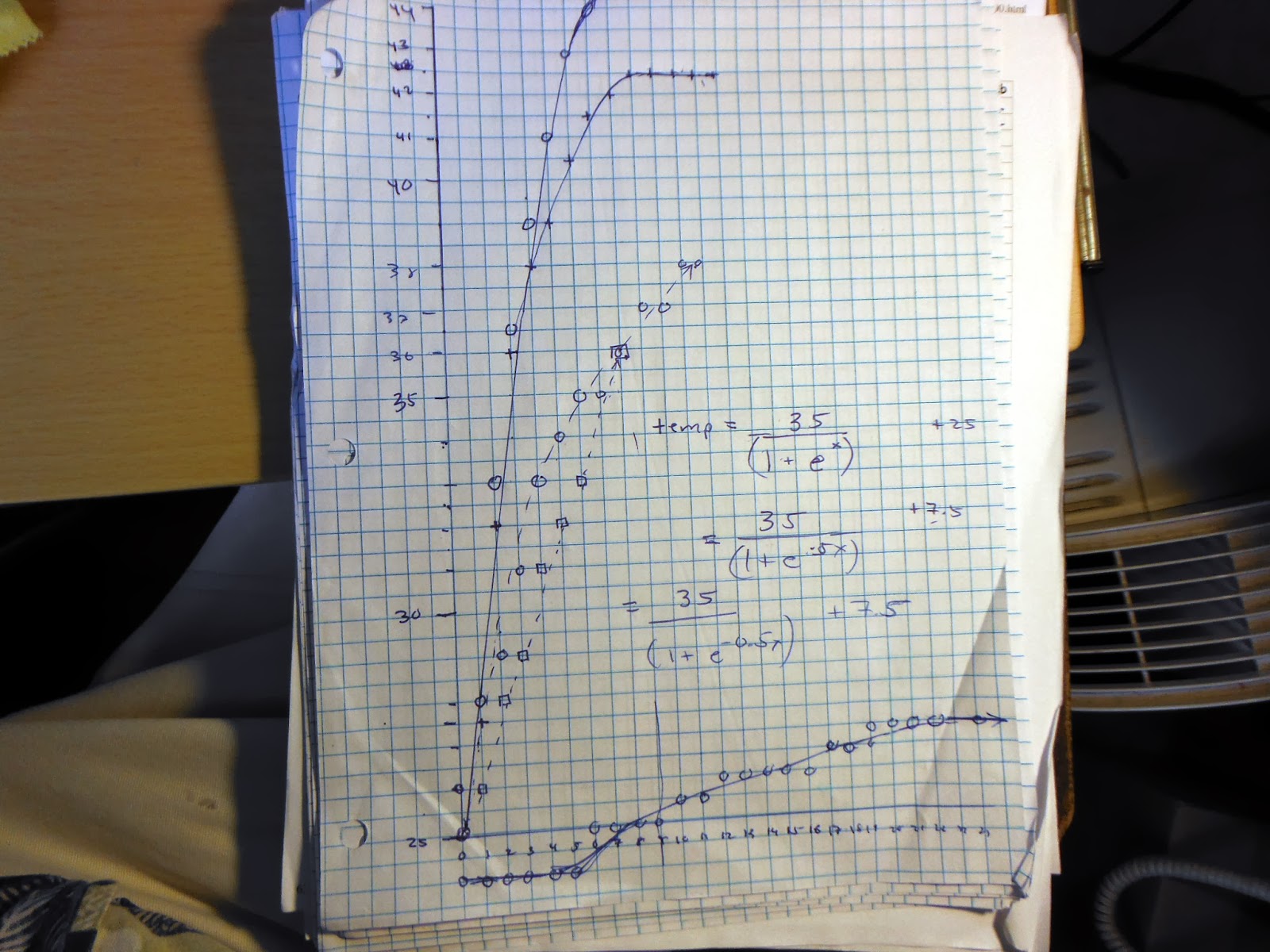
The function is a logistic function, but not in a probability format. The starting structure is essentially (y - k) = range/(1-e^(-a(x-h))) where k is the start value and h is the x-value at the middle of the rise in temperature. Note that for some groups the best fit is achieved by calling (0, 25) the middle of the rise i temperature. This puts the theoretic start value at 25-(maximum-25), if 25 is the start value. I know that can be reduced, but then the meaning is lost.

Ideally the system holds at the starting temperature, then the range is the vertical span of the logistic function.

The coefficient a is found by trial and error, this affects the speed of the rise. Values of 0.6 to 0.8 appear to generate best fits. The actual function in spreadsheet cell C2 is =F$3/(1+EXP(-F$8*(A2-F$7)))+F$1 where F$3 contains the vertical range, F$8 contains the coefficient, F$7 contains the midrise time, and F$1 contains the start value. A2 holds the time.

Comments

Post a Comment

Popular posts from this blog

Plotting polar coordinates in Desmos and a vector addition demonstrator

Image
In an earlier post I noted that Desmos did not directly plot polar coordinates. Not only was I incorrect, but Desmos responded to my blog to correct me! Although I had at some point seen that one could define a function f(x)=3x+5 and then have Desmos calculate f(6), I had not absorbed how this might be used to plot polar coordinates. The above works beautifully . Realizing that I could effectively program Desmos, I applied this thinking to demonstrating how to add two vectors when given the magnitudes m and the direction angles theta. The graph calculates the i and j components for the two vectors and then adds the vectors, graphically displaying the result while also providing information on the magnitude and direction of the vector sum. m1 and theta1 are the magnitude and direction angle for one of the two vectors, m2 and theta2 are the magnitude and direction for the other vector. All four are dynamically interactive and can be changed. The diagram purports to illustra
Read more

Setting up a boxplot chart in Google Sheets with multiple boxplots on a single chart

Image
The  Google Statistics  add-on for Google Sheets can display multiple boxplots in a single chart. The key is the layout of the data. One column should be the variable by which the data is to be grouped, the other column should be the data to be box plotted. Set up the Statistics add-on with the data to be plotted as the variable, and the grouping column as the "by" variable. In this image I had deselected all but the boxplot option, the result was the appearance of the Moment, Standard errors, and Confidence intervals options. The default is apparently a 95% confidence interval for the mean. The result is multiple boxplots on a single chart with a common scale. The new tab that is created also quotes 95% confidence intervals for the mean. Note that as of 2018 the Google Statistics add-on cannot be found by search in the add-ons. In addition, as of May 2018 the add-on no longer verifies, possibly due to the add-on not having been updated since August 2017. One may ha
Read more

Traditional food dishes of Micronesia

Image
Clara, Jennette, and Joanie presented ground hard taro cooked in an umw, effectively a hot rock oven. Pohnpeian: rotama. Pingelapese: sero. Mwoakillese: rodma. Mortlockese: Amahd. Kosrae: rodoma. After cooking in an umw the rotama is pounded with the petiole of a palm frond. Rotama is made from hard or swamp taro, known as mwahng on Pohnpei, mweian on Pingalap, pula in Mortlockese, and pahsruhk on Kosrae. In traditional times on the outer islands the women had primary responsibility for tending the taro while the men handled fishing and climbing tasks. Joesen and Noeleen presented fermented breadfruit from the outer islands of Yap such as Woleai and Eauripik. The raw ingredients were actually brought in from Yap, Noeleen prepared the maare.  The leaf wrap is ti leaf - Cordyline fruticosa. Pauleen, Barnson, Trisha, Verginia, Con-ray, and Maylanda from Kitti, Pohnpei brought in mahi umw, koahpnoair koakihr, and uht sukusuk. Above is breadfruit umw, mahi umw, one o
Read more