Site swap mathematics
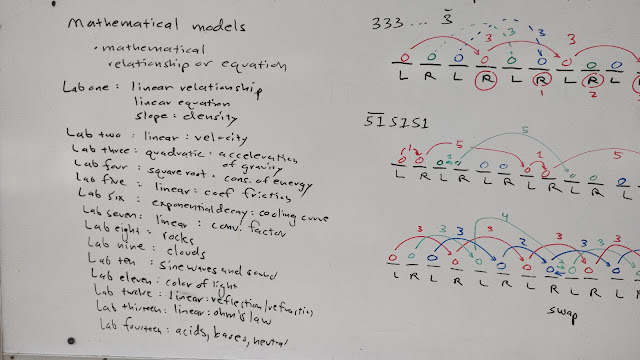
The opening this term was altered to focus on laboratories rather than the math stack. This allowed me to better juxtapose the uselessness of quadratic equations for my non-science major students with the usefulness in describing acceleration. Mathematics has a use but much of what we teach students has no use in their lives. Not until their own children come home from high school and say, "Mom, I know you went to college. Can you help me with my algebra homework?" If useless mathematics is what is being taught - never mind the contrived "real world" and "application" problems in textbooks - what does it matter which form of useless mathematics is taught? Might as well teach the students site swap notation. Will they ever need to use site swap notation? No. But the same can be said of the quadratic formula, especially for students who are business, elementary education, and social science majors. Then I introduced site swap in the


