Newton's laws from a momentum perspective, force, and pulleys
On Monday I again tried using a hanging mass at the end of a rope to attempt to accelerate my RipStik as a way of demonstrating both the conversion of gravitational potential energy to kinetic energy and the effect of a force, F = mg, to produce an acceleration of a RipStik and rider.
I used a 2 kg hand weight has a handle for the construction twine - not an ideal cordage. A more significant rope has been purchased for next term, fifty some feet. Maybe I can use the length of the classroom or an outdoor location. porch. I managed to prop myself up on my RipStik against the north wall, holding the handle in one hand and my stop watch in the other.

I made some initial runs without stopping, showing that the ball and I travel together, the ball does not fall. Then I stepped off the RipStik and came to a sudden stop.
This lab goes more smoothly than the Hooke's law lab with marbles. Maybe this lab should be shifted to balancing marbles - some kind of split aerial pulleys with a block and tackle on one side to permit cups with less marbles to balance cups with more marbles. Then the actual mechanical advantage would be the ratio of marbles, which could be obtained from the slope. Might be fun, although a lot of marbles would be needed. This would also make the lab a little more local.
Three 2 kg masses were hung rather precariously on a 50 g mass hangar.
The basic layout and energy calculations are seen above. The drop height was 0.6 meters, gravity was taken as 9.8 m/s², and the mass was six kilogram for a gravitational potential energy of 35 Joules. After being pulled, I used a tape measure on the floor to measure my post-acceleration coasting speed for 100 centimeters. I covered the one meter in 1.38 seconds for a speed of 0.72 m/s and a kinetic energy of 17 Joules. 18 Joules were lost to a variety of sources including friction of the rope on the table, rolling resistance of the floor, timing errors, and plain old uncertainty in measurement.
The force of the masses was 58.8 Newtons (which should probably have been calculated first so that the GPE would be the Force through the Distance (58.5 times 0.6).
I then did some timing runs for the accelerated portion of the run and found a time of 1.66 seconds. I used this, my mass of 67 kilograms, and my final velocity of 0.72 m/s to calculate my change in momentum per unit time. When I was done I came up with 28.9 Newtons of force on the RipStik.
I suspect that I might have only left the students perplexed. I probably should not have started off from energy considerations, although I was trying to provide a connection to the energy work of the prior term. I should have simplified and just ran calculations on the forces involved. The masses are clearly F = mg, the second part should have been a more straightforward calculation of the force on the RipStik.
On Wednesday I decided to forgo the classroom and cover Newton's laws from a momentum perspective outside, using the new solar panel covered sidewalk as that cement is particularly smooth.
I began with Newton's first law thought of in momentum terms where p is the momentum, Δp = 0. For Δp = 0 one solution is the velocity is zero. An object at rest tends to stay at rest. I then noted that Δp = 0 can also be obtained where the start and end momentum are the same. This can happen when the velocity is a constant. An object in motion tends to remain in motion. Unless acted on by outside forces - but those would violate Δp = 0.
I stood stationary with the ball on my hand, steadying myself with a solar panel post. Then I rode at a constant velocity holding the ball in the palm of my hand.

I made some initial runs without stopping, showing that the ball and I travel together, the ball does not fall. Then I stepped off the RipStik and came to a sudden stop.
Rickson captured this excellent photograph of the ball bouncing away down the sidewalk - continuing at a constant velocity. No external force acted on the ball, the ball tended to remain in motion.
Setting aside the ball, I then moved on to Newton's second law. I accelerated for the first two posts and then coasted for the next two posts, clicking off times as I went. The posts are 501 centimeters centerline to centerline, but I called them 5 meters even to simplify calculations.
Rickson continued to document the activity photographically. I then ran calculations on my yellow pad while sitting at a post.
The catch was the calculation were still very complex with multiple steps. I need to work on simplifying this process, maybe just working on a single acceleration across ten meters, ignore the coasting phase, and do not generate separate forces for the two five meter segments.
Unfortunately all the students could see was the top of my head.
Only when I tried to commit the four post sequence to paper did I realize just how complex the chains of calculation were. Click to enlarge the image.
The first five meters were shaky, I was not yet stably on the board as I started from zero m/s. After five meters I was more stable and was driving harder into the board. Thus the force rose from 24.7 N to 35.0 N.
On Thursday the class made measurements of actual mechanical advantage for pulley systems.
This lab goes more smoothly than the Hooke's law lab with marbles. Maybe this lab should be shifted to balancing marbles - some kind of split aerial pulleys with a block and tackle on one side to permit cups with less marbles to balance cups with more marbles. Then the actual mechanical advantage would be the ratio of marbles, which could be obtained from the slope. Might be fun, although a lot of marbles would be needed. This would also make the lab a little more local.


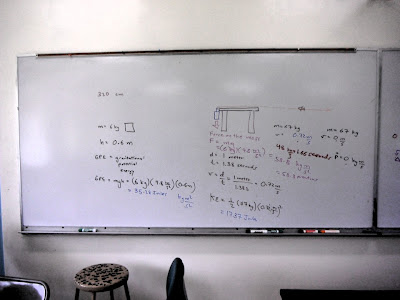












Comments
Post a Comment