Site swap notation
The last physical science laboratory of the term seeks to bring home the meaninglessness of the manner in which mathematics in taught in schools at present.
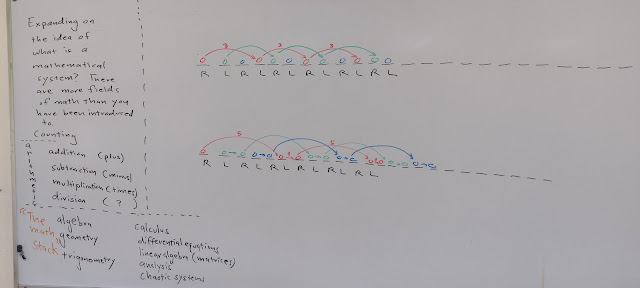
I start off my outlining the "math stack" from counting through arithmetic, algebra, and on up through calculus and beyond. I note that there are other fields of mathematics that do not make it into the stack, and yet they are no more useless to the average liberal arts major than knowing how to factor a quadratic equation. Because factoring quadratics is not a useful life skill. There are far fewer people on the planet getting paid to factor quadratic equations as a living than there are people who are paid to play video games for a living (check out the Asian competitive video game playing scene).
Then I lay out the patterns seen on the board and ask the students to predict the next letter, colored circle, arrow, or number in the sequence. Today all of the students were successful in answering my questions. I even ran a 42 site swap into the top equation and showed how that changed the order of the colored circles. I then suggested to the class that they could take and pass a quiz on the sequences, I could assess their learning of the patterns, and then I could report to my administration that the students had mastered site swap mathematics. And everyone would be happy. Without anyone understanding anything about the system, what it is useful for, or whether they would ever need to use the system again in life. And that is exactly what we do in algebra class. Teach an abstract system of making marks on pieces of paper, quiz the students on making the right abstract marks, and then the students never need to make those marks again until their future child comes home from high school needing help on their algebra one homework.
Sure, there are professions that do math, but none do "thirty problems, even numbers only" That is an Italian mathematicians competitive gambling game. No one who actually uses mathematics does so in the fashion in which mathematics is taught in schools. The way mathematics is taught in the schools is akin to teaching the fine art oil painting by having the students paint a white picket fence. There is no relationship there. Little wonder most students are happen to have completed their mathematics requirement and never see another equation again.
I teach one equation a week, an equation that arises from data gathered in class, an equation that models an actual concrete, physical system. One equation. Real data. Real meaning.
With that introduction, I then proceed to produce the concrete, tangibles of site swap mathematics. Juggling. I demonstrated a 3, a 51, and the 42 swap.



























Comments
Post a Comment