Day four acceleration and the arc of a ball

 I opened day four by taking the students back through the graphs for the first three days. 

I took care to point out that all week we had examined time versus distance. I emphasized that on day four we would be looking at space versus space, horizontal versus vertical. I demonstrated a ball arc in front of the board and asked the shape the ball's path would trace out. One student suggested a circle. Another suggested a parabola. I then had the students, working in pairs, trace ball arcs on the board.

Six groups were up at the board. 

Three pairs on the right, three on the left. 

Jasmine working on her ball arc with Jessie May. 

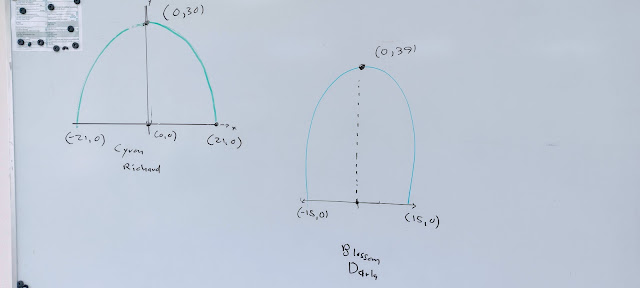
After the students had sketched their arcs, I added in an x-axis. Splitting the distance between the x-intercepts in half, I wrote the coordinates of the x-intercepts. I also measured the height of the vertex above the x-axis, with all measurements being done in centimeters using a meter stick. 

A circle as being the shape was ruled out by the shapes seen on the board. 

I asked the students to work on finding an equation for their arc. I assigned the students who were not in an arc drawing group to one of the existing groups. I gave them no more directions than to find an equation that would produce their arc.

Bear in mind that almost all of the students have completed MS 100 College Algebra and many have completed MS 101 Algebra and Trigonometry. If nothing else one might expect that a student would realize that the x-intercepts are the solutions and build factors from there. That would get them at least part way to an equation. 

These students realized that they needed a quadratic. They they entered the equation into Desmos. 

Here a student has written the vertex form of the equation, the approach an experienced mathematician might take. Whether that 2 is an exponent or not is not clear.

This pair started with the quadratic formula, or a variation of the quadratic formula, but also went on to write down the vertex form and the quadratic form.

Forging ahead with a variation on the vertex form, without the "a" coefficient on the (x-h) term. The student did realized that h was zero and k was 39. 

I made no rules, stated no boundaries. This pair tried Internet searches but the formulas they found were useful only for solving quadratic equations, not building the equations from a graph.

Another student working with a variation of the quadratic formula. Unclear whether the -b term is over 2a or not.

The one group that used Desmos to set up an equation set up sliders and then used the sliders to find the equation that went through the points. I thought this was brilliant. I had not said one could not use Desmos, so they turned to Desmos. Desmos' ability to explore mathematics in an almost tactile fashion is unique. 

Algebra as taught remains lost in algorithms and working problems one to thirty even numbers only. The result is not students who can think mathematically. And the goal of algebra education is unclear given that so few students go on to actually use algebra in life. I asked my students again today whether they consider themselves good at math. None said they were, although I am aware that a couple students are "good at math" as measured by the traditional curriculum. I asked one if she like math, she said no. I then told the class that they can do math, they are good at math, they are just not good at memorizing algorithms for hand working problems. Along the way the beauty of math, the surprising effectiveness of mathematics, is lost on the students. 

Today a roomful of students engaged with mathematics pursuing solutions.